Backtracking solve Subset/Combination/Permutation

Backtracking is a general algorithmic technique that is used to solve a variety of problems that involve searching through all possible solutions to find the best one.

Backtracking template:

result = []

def backtrack(Path, Seletion List):
    if meet the End Conditon:
        result.add(Path)
        return

    for seletion in Seletion List:
        select
        backtrack(Path, Seletion List)
        deselect

Can be used to solve these common problems:

1. Subset (Leetcode 78)

Input: nums = [1,2,3]

Output: [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

var subsets = function (nums) {
  const res = [];
  var backtrack = function (track, start) {
    res.push([...track]);
    for (let i = start; i < nums.length; i++) {
      track.push([nums[i]]);
      backtrack(track, i + 1);
      track.pop();
    }
  };
  backtrack([], 0);
  return res;
};

2. Combination (Leetcode 77)

Input: n = 4, k = 2

Output: [[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]

var combine = function (n, k) {
  const res = [];
  var backtrack = function (track, start) {
    if (track.length === k) {
      res.push([...track]);
      return;
    }
    for (let i = start; i < n; i++) {
      track.push(i + 1);
      backtrack(track, i + 1);
      track.pop();
    }
  };
  backtrack([], 0);
  return res;
};

3. Permutation (Leetcode 46)

Input: nums = [1,2,3]

Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

var permute = function (nums) {
  let res = [];
  var backtrack = function (track) {
    // goal
    if (track.length === nums.length) {
      res.push([...track]);
      return;
    }
    for (let i = 0; i < nums.length; i++) {
      if (track.includes(nums[i])) {
        continue;
      }
      track.push(nums[i]);
      backtrack(track);
      track.pop();
    }
  };
  backtrack([]);
  return res;
};

4. Generate Parentheses (Leetcode 22)

Input: n = 3

Output: ["((()))","(()())","(())()","()(())","()()()"]

var generateParenthesis = function(n) {
    const res = [];
    var backtrack = function(track, open, close) {
        console.log(track);
        if (track.length === n*2) {
            res.push(track);
            return;
        }
        if (open < n) {
            backtrack(track + "(", open+1, close)
        }
        if (close < open) {
            backtrack(track + ")", open, close+1)
        }
    }
    backtrack([], 0, 0);
    return res;
};

5. Combination Sum (Leetcode 39)

Input: candidates = [2,3,6,7], target = 7 Output: [[2,2,3],[7]]

var combinationSum = function(candidates, target) {
    const res = [];
    const backtrack = function(track, start, sum) {
        if (sum === target) {
            res.push([...track]);
            return;
        }
        for (let i = start; i < candidates.length; i++) {
            if (sum + candidates[i] > target) {
                continue;
            }
            backtrack([...track, candidates[i]], i, sum + candidates[i])
        }
    }
    backtrack([], 0, 0);
    return res;
};

6. Word Search (Leetcode 79)

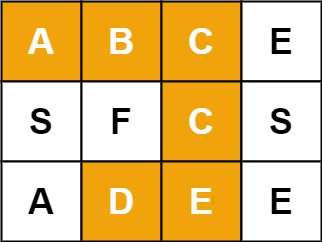
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED" Output: true

var exist = function (board, word) {
    const rows = board.length;
    const cols = board[0].length;

    var backtrack = function (index, x, y) {
        // meet the target
        if (index === word.length) {
            return true;
        }

        if (x >= cols || x < 0 || y >= rows || y < 0 || board[y][x] !== word[index]) return false;

        const temp = board[y][x];
        board[y][x] = "#";

        const found = backtrack(index + 1, x + 1, y)
        || backtrack(index + 1, x, y - 1)
        || backtrack(index + 1, x, y + 1)
        || backtrack(index + 1, x - 1, y);

        // restore;
        board[y][x] = temp;

        return found;
    }

    for (let i = 0; i < rows; i++) {
        for (let j = 0; j < cols; j++) {
            if (board[i][j] === word[0] && backtrack(0, j, i)) {
                return true;
            }
        }
    }

    return false;
};

Refs:

https://labuladong.gitbook.io/algo-en/iii.-algorithmic-thinking/subset_permutation_combination